I spent the weekends of a weird month writing a computer program to multiply matrices quickly. Matrix multiplication makes up the majority of the computational effort in getting ChatGPT to talk, so considerable human effort has gone into making it fast. Thanks to this, the matrix multiplication here does ~2.5 trillion 32-bit floating point operations a second while computing the product of two $4000\times 4000$ matrices on my 2022 MacBook Air.

There is a bona fide canon of good blog posts about fast matrix multiplication programs, this having the dubious distinction of being the first about an Apple GPU. The program resembles Philip Turner and Liu Liu's excellent metal-flash-attention implementation and, in turn, has performance on par with Apple's closed-source Metal Performance Shaders (MPS) matrix multiply.

Achieving MPS-level performance requires using an undocumented instruction, simdgroup_async_copy. Section II describes how to use it, then how to make it fast with a counterintuitive microbenchmark. Section III describes the matrix multiplication program. Section I gives background on tiled matrix multiplication and how GPUs work.

I - Background

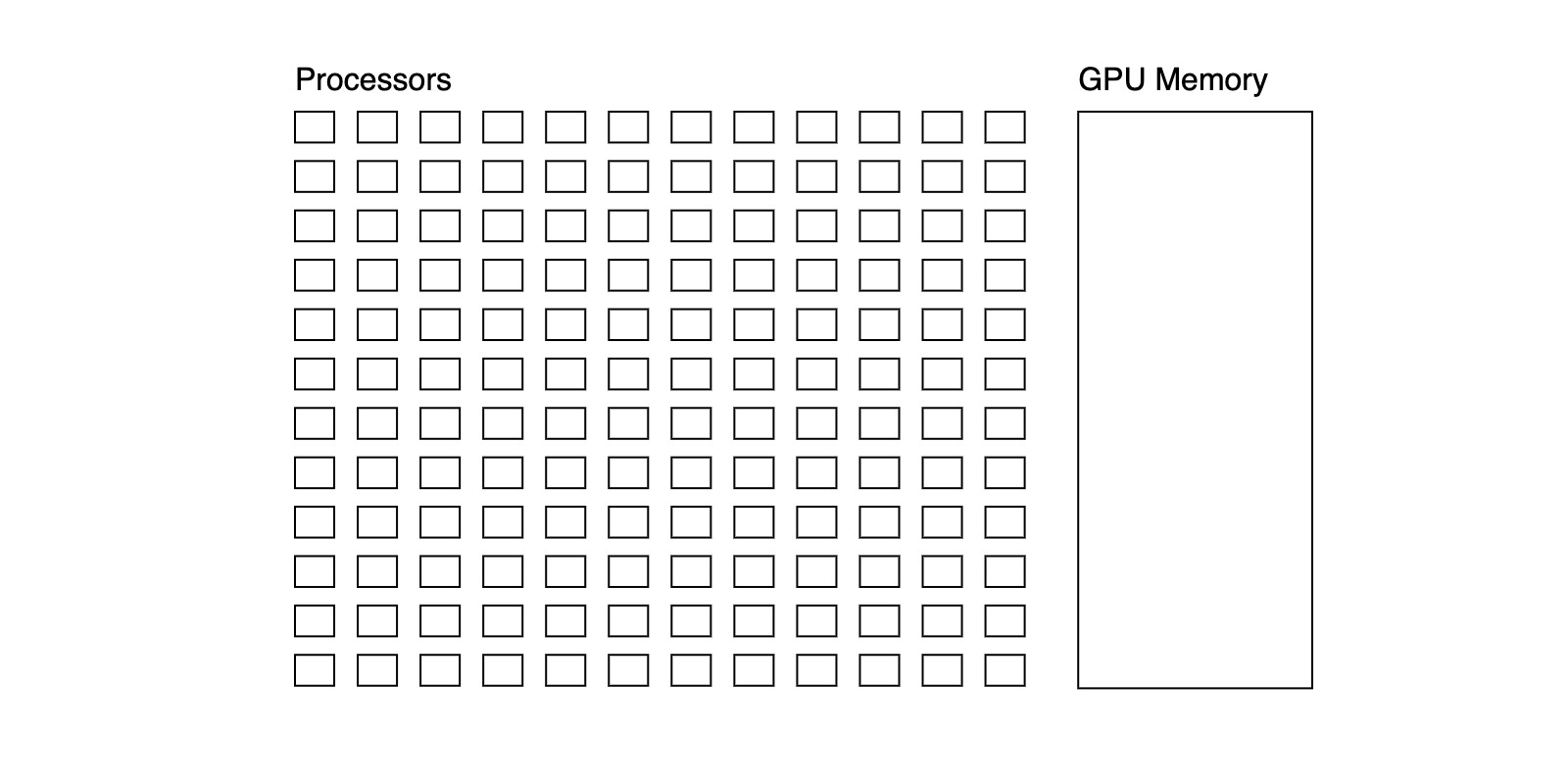
A GPU is a collection of processors and some GPU memory. Processors execute instructions on multiple pieces of data simultaneously (this is called SIMD execution), for example one can do $1+2$ and $2+3$ simultaneously with a plus instruction, but can't do $1+2$ and $2\cdot 3$ simultaneously because plus and multiply are different instructions. Processors have fast access to GPU memory, but reading data from the rest of the computer, hereafter device memory, is comparatively slow.

If a processor can execute instructions on $k$ pieces of data simultaneously, we'll say it is composed of $k$ threads. When programming a GPU, you write programs for threads. If threads in the same processor end up executing different instructions, you pay a performance cost to emulate this on the SIMD runtime.

In the GPU programming abstraction, threads are organized into threadgroups which share access to threadgroup memory. To map this to hardware, threadgroups cannot consist of more threads than are on the GPU, and a threadgroup's memory cannot be larger than GPU memory. When a program runs, as many threadgroups as possible are loaded onto the GPU and executed simultaneously. Finished threadgroups are swapped with unfinished ones. In hardware, threadgroup memory corresponds to GPU memory, so working with threadgroup memory is faster than device memory.

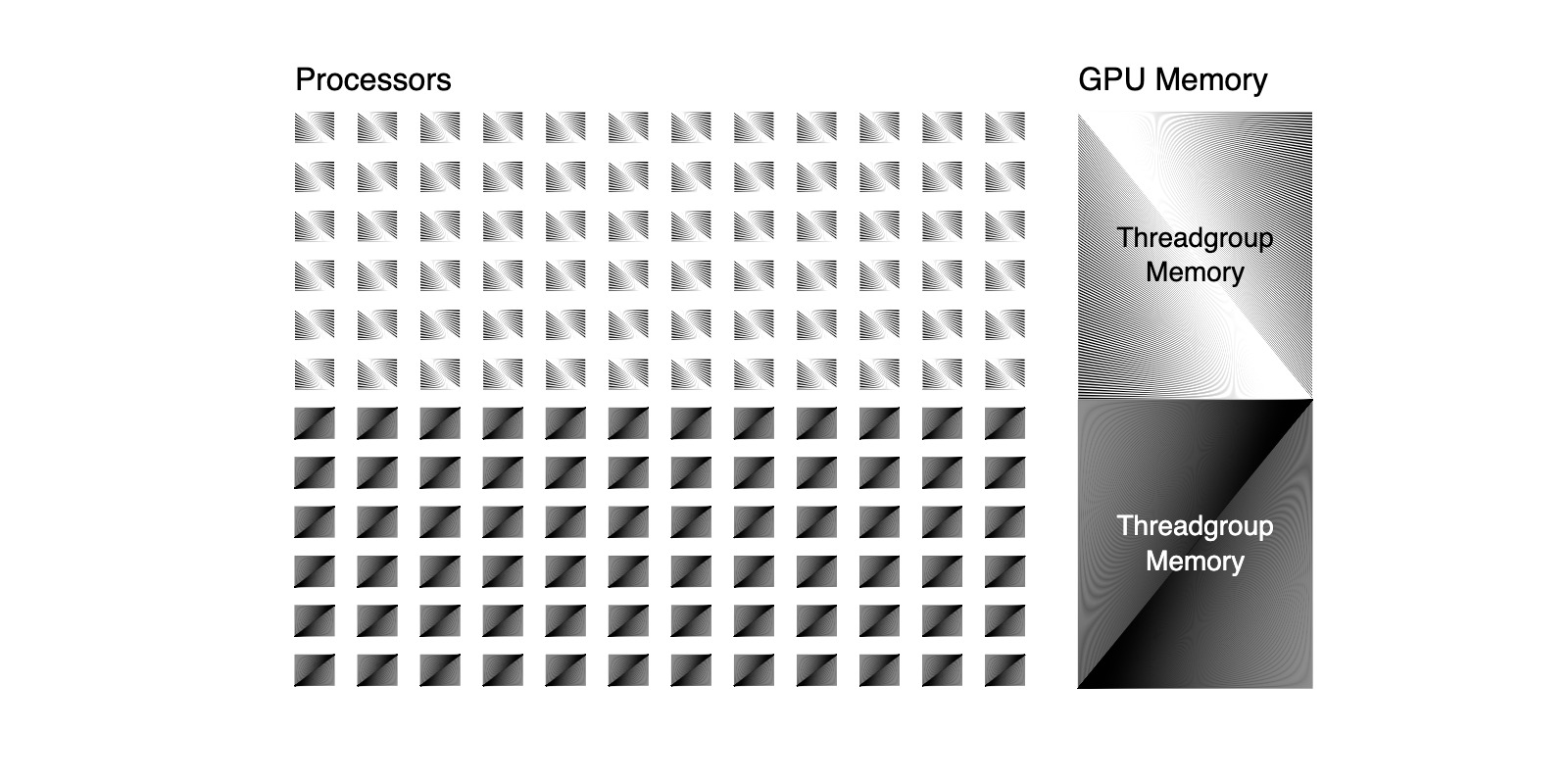
For example, in the illustration above, two threadgroups are mapped onto the GPU simultaneously. Because these threadgroups are using every processor on the GPU, if either required one more processor, together they would require more processors than are available, so only one could run at a time: Bigger threadgroups are not always better.

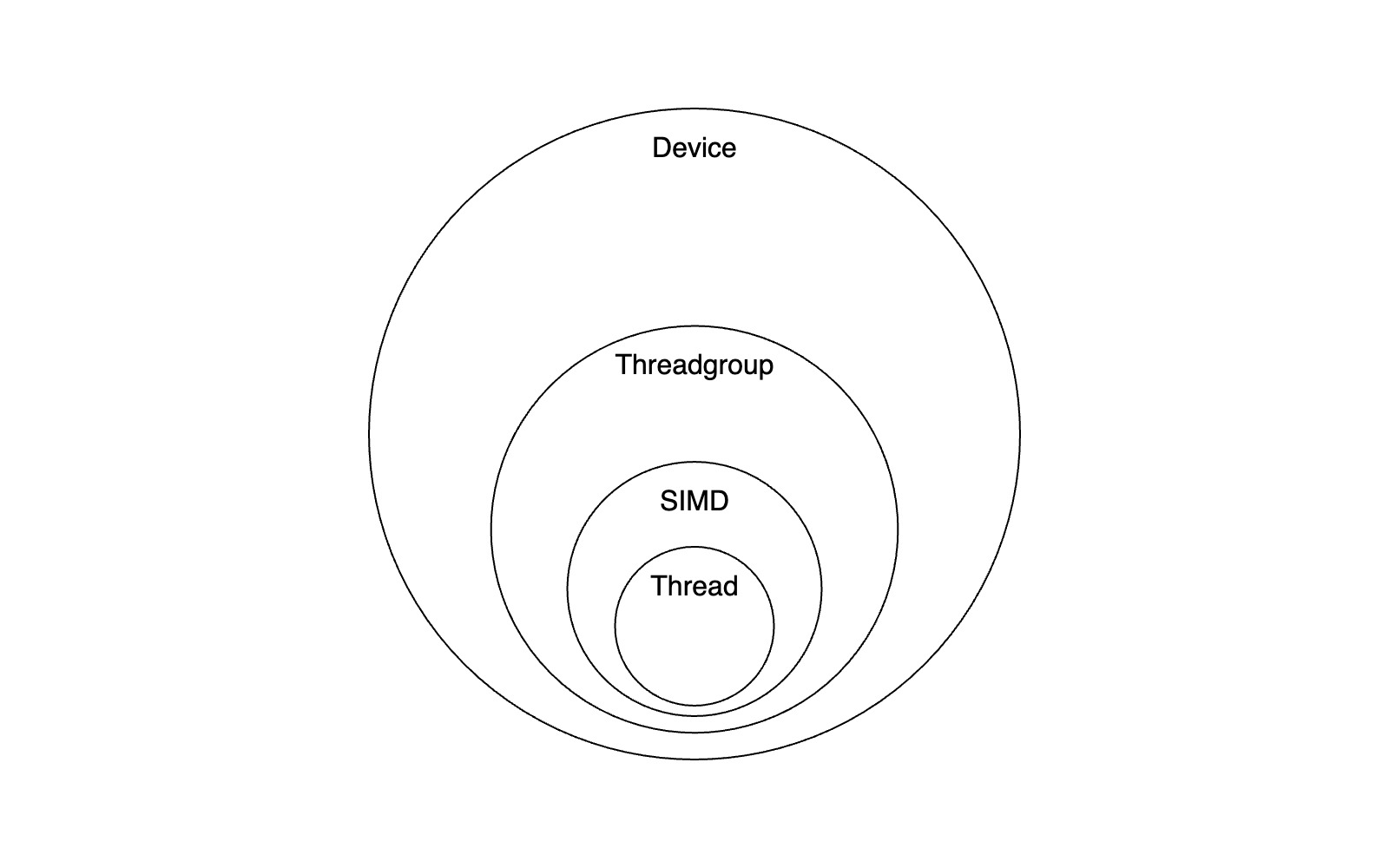
This all comes together into a hierarchy like the one above. The smallest unit of computation is a thread. Threads execute on SIMD processors, are grouped into threadgroups, and have fast access to threadgroup memory. Things that can't fit in threadgroup memory live elsewhere on the device and are comparatively slow to access.

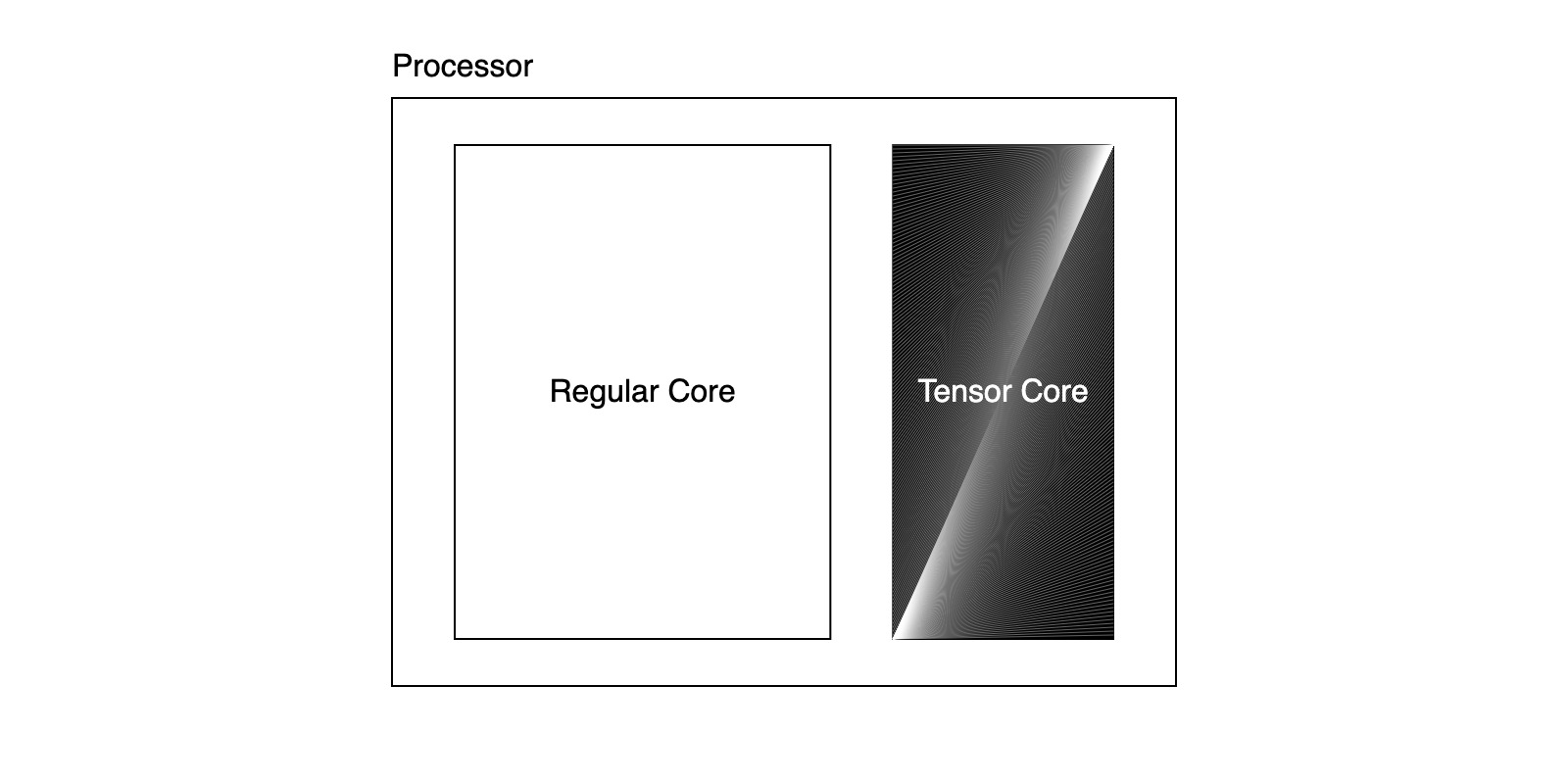
To make operations like matrix multiply fast, modern GPU processors have an additional feature called tensor cores: special hardware for linear algebra. The one on Apple GPUs can do $8\times 8$ matrix multiplication. Using a tensor core is much, much faster than doing the corresponding arithmetic, but requires all the processor's threads to collaborate. While the regular programming abstraction allows threads on a processor to execute different instructions with an emulation cost, all the threads on a processor must collaboratively run the tensor core or it will not work.

I.I - Tiled Matrix Multiply

The performance of tensor cores means that to write an efficient matrix multiply we will need to decompose matrix multiplication into $8\times 8$ matrix multiplication. This is, fortunately, easy.

For example, consider the following two matrix multiplications and how they yield similar output.

In the second multiplication, the matrices are changed into matrices of $2\times 2$ matrices, but the result is effectively the same. These $2\times 2$ matrices are called tiles and this example isn't a quirk: Any matrix multiply can be broken down into multiplication of tiles. This is how matrix multiplication is reduced to $8\times 8$ matrix multiplication for tensor cores.

For a more formal perspective, let $\mathbb{R}^{n\times m}$ denote the set of matrices of real numbers with $n$ rows and $m$ columns and suppose we have matricies $A\in\mathbb{R}^{\alpha n \times \beta k}$ and $B\in\mathbb{R}^{\beta k \times \gamma m}$ composed of tiles with shapes $\alpha\times\beta$ and $\beta\times\gamma$ respectively. Letting $A^{(i,j)}$ denote the $j$th element of the $i$th row of $A$'s tiles, the $l$th element of the $k$th row of $A^{(i,j)}$ is

and letting $B^{(i,j)}$ be defined likewise

we can write the formula for elements of $AB$ in terms of the product of their tiles:

So the product of any two matrices divisible into $8\times 8$ tiles can be computed via multiplications of the tiles. This is how small tensor cores are used to compute large matrix multiplies.

Exercise 0. Does tiling change the number of arithmetic operations on elements of $A$ and $B$ needed to compute $AB$?

I.II - Threadgroup Tiling

With another level of tiling we can make use of threadgroup memory.

The $j$th element of the $i$th row of $C$, $C_{i,j}$, in $C=AB$ is the dot product of the $i$th row of $A$ and $j$th column of $B$. Suppose processor P0 is computing $C_{i,j}$ and P1 is computing $C_{i,j+1}$, naively both will load row $i$ of $A$ from device memory into their tensor core, but if P0 and P1 are in the same threadgroup they could collaborative load row $i$ of $A$ into threadgroup memory, then load row $i$ of $A$ into their tensor cores. Because loading from threadgroup memory is comparatively fast, this collaborative loading is more efficient than independently loading row $i$ of $A$ from device memory.

I have done my best to illustrate this situation. Below, P0 computes $C_{1,1}$ and P1 computes $C_{1,2}$. The elements of $A$, $B$, and $C$ that P0 needs to access to compute $C_{1,1}$ are filled in with a $\backslash\backslash$ pattern and the elements needed by P1 are filled in with a $//$ pattern. The row of $A$ shared by P0 and P1 has a cross-hatched pattern, the result of overlapping P0 and P1's patterns. Because this row of $A$ is used by both P0 and P1, it is efficient to collaboratively load it into threadgroup memory rather than independently load it from device memory.

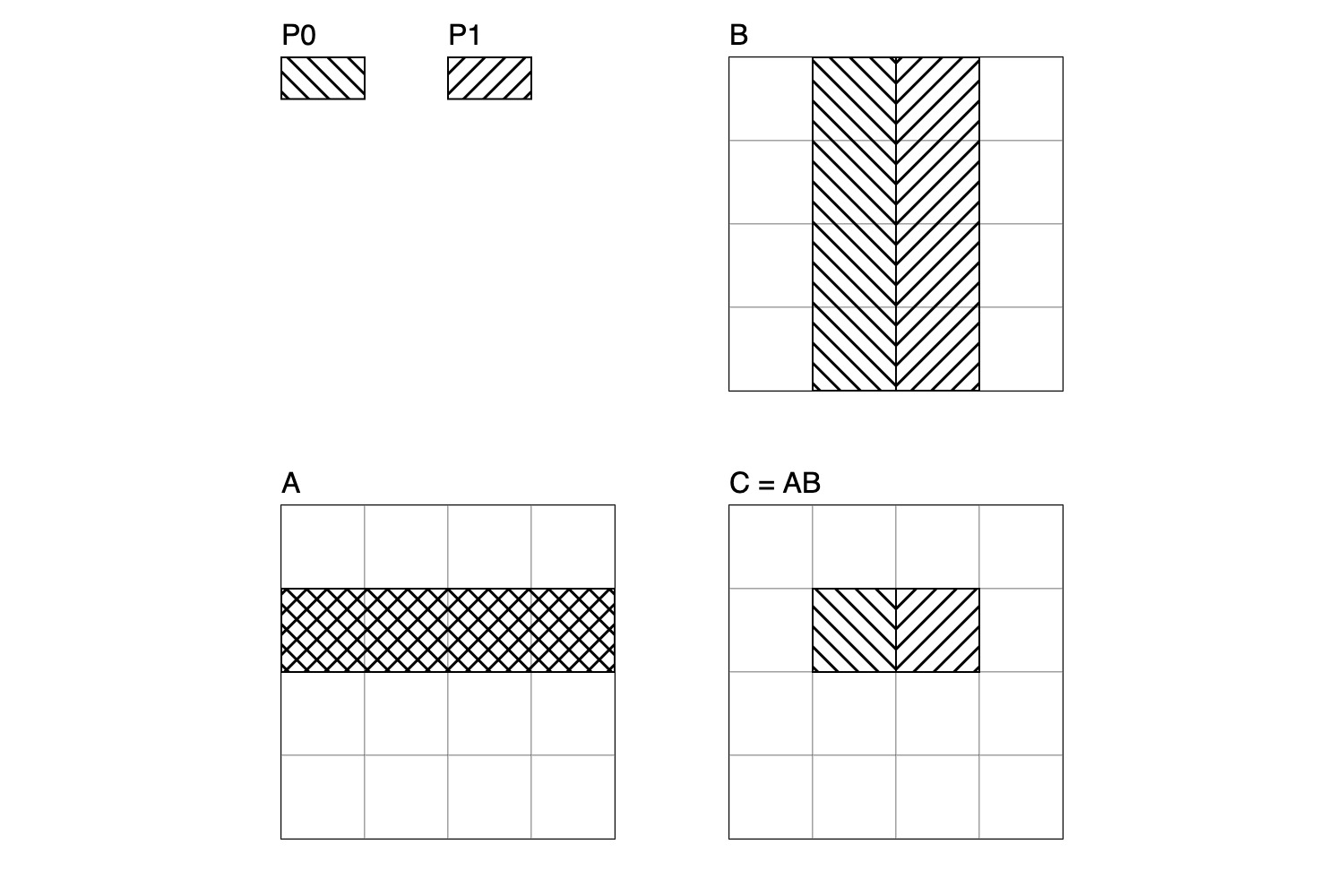
In conclusion, our tiled matrix multiply will decompose computation of the product of $A\in\mathbb{R}^{\alpha n 8 \times \beta k 8}$ and $B\in\mathbb{R}^{\beta k 8 \times \gamma m 8}$ into computation of the product of $8n\times 8k$ tiles of $A$ and $8k\times 8m$ tiles of $B$ with threadgroups. Each threadgroup will collaboratively load overlapping rows and columns of $A$ and $B$ into threadgroup memory, then decompose the computation of the product of tiles into the product $8\times 8$ subtiles which can be executed on tensor cores.

Exercise 1. What happens when the overlapping rows and columns of $A$ and $B$ are larger than threadgroup memory? Hint: Break them up into tiles.

Exercise 2. What happens when $A$ and $B$ have shapes that aren't divisible by $8n\times 8k$ and $8k\times 8m$ tiles? Hint: How does padding $A$ and $B$ with zeros change the result? What if you can't zero-pad? Think carefully about how if statements interact with non-SIMD emulation overhead.

II - simdgroup_async_copy

This blog post will stop making sense now without basic familiarity writing GPU programs and with Apple's Metal programming language.

Implementing an efficent matrix multiply on an Apple GPU requires an undocumented instruction for copying data from device to threadgroup memory: simdgroup_async_copy. Calling it is a matter of adding the code below to your kernel. I've added annotations to the arguments whose purpose I fully understand.

struct _simdgroup_event_t;
thread _simdgroup_event_t* __metal_simdgroup_async_copy_2d(
  ulong,               // sizeof(element)
  ulong,               // alignof(element)
  threadgroup void *,  // destination
  ulong,               // elements_per_row
  ulong,
  ulong2,              // tile_size (cols,rows)
  const device void *, // source
  ulong,
  ulong,
  ulong2,
  long2,
  int)
  __asm("air.simdgroup_async_copy_2d.p3i8.p1i8");

Because this copy happens asynchronously, the returned struct _simdgroup_event_t needs to be waited on before reading from the loaded memory. This is accomplished with the function below.

void __metal_wait_simdgroup_events(
  int, // len(events)
  thread _simdgroup_event_t**
)
  __asm("air.wait_simdgroup_events");

To make calling the copy easier, I use this helper function that takes the size of a tile as a template parameter.

template<
  ushort tile_cols,
  ushort tile_rows
>
inline thread _simdgroup_event_t* simdgroup_async_copy(
  const device float* src,
  const ushort2 src_pos,
  const ushort2 src_shape,
  threadgroup float* tile) {
  src = src + src_pos.x+src_pos.y*src_shape.x;
  return __metal_simdgroup_async_copy_2d(
    sizeof(float),
    alignof(float),
    reinterpret_cast<threadgroup void*>(tile),
    ulong(tile_cols),
    1,
    ulong2(tile_cols, tile_rows),
    reinterpret_cast<const device void*>(src),
    ulong(src_shape.x),
    1,
    ulong2(tile_cols, tile_rows),
    long2(0),
    0);
}

The simdgroup_async_copy instruction has somewhat counterintuitive performance characteristics. Whereas the previous section suggested processors in a threadgroup could collaboratively load shared rows and columns of $A$ and $B$ while computing $AB$, in practice it is much faster to have a single processor do the loading. The graph below shows the results of a microbenchmark demonstrating this phenomenon. In the benchmark, the entirety of threadgroup memory is filled with data from device memory; along the x-axis the number of processors that collaborate to load the memory is varied (with $n$ processors, each loads $1/n$th of the memory, with the $i$th processor loading positions $[i/n,(i+1)/n)$). The y-axis reports runtime.

I can only speculate as to why this occurs. One observation from my benchmarking is, when the async copy instruction runs, several integer instructions are dispatched to the ALU (I suspect to compute indexing information for the copy). On my M2 GPU, integer instructions are very expensive, so possibly the integer overhead is large enough to eclipse any performance advantages from multiple processors performing the load simultaneously.

III - The Matrix Multiply Program

We now have all the background needed to describe the matrix multiply program.

Programs run on Apple GPUs are parameterized by grid and threadgroup sizes. For example, when multiplying a $n\times k$ and $k\times m$ matrix to make a $n\times m$ matrix, the grid size might be $(m,n,1)$ (Apple convention is shapes being $(\text{columns}\times\text{rows})$) and the threadgroup size $(10,10,1)$, indicating that each threadgroup is responsible for a $10 \times 10$ tile of the result and consists of $10\cdot 10=100$ threads. Grid and threadgroup sizes are three-dimensional, hence the $1$ dimension in the example. We can use this to make reasoning about SIMD processors easier.

In the kernel below, each SIMD processor is responsible for a $(8s)\times (8s)$ tile of $C$ while computing $C=AB$. Each threadgroup is made up of a $\sigma\times\sigma$ grid of SIMD processors, and in turn is responsible for a $(8s\sigma)\times (8s\sigma)$ tile of $C$. Supposing $A$ and $B$ have dimensions $n\times k$ and $k\times m$ and $n$ and $m$ are divisible by $8s\sigma$, and letting $w$ denote the number of threads in a SIMD processor our grid size is $(w, m/(8s), n/(8s))$ and our threadgroup size is $(w,\sigma,\sigma)$.

When the program is dispatched, the first $w$ threads will have $(y,z)$ position $(0,0)$, the next $w$ $(1,0)$, and so on. In turn, if $\texttt{pos}$ denotes the grid position of the current thread, then $\texttt{pos.yz*}8\texttt{*}s$ is the upper-left corner of the tile of $C$ the thread's processor is responsible for. This makes it very easy to write SIMD code, because so long as $\texttt{pos.x}$ is never read, no thread will ever learn its position in the processor's SIMD group, and in turn all threads on a processor will act in lockstep by construction.

With all of this said, the matrix multiply program of this blog post is below. For input matricies $A$, $B$, and $C$ of size $n\times k$, $k\times m$, and $n\times m$ the program computes $\alpha AB+\beta C$ and stores the result in the $C$ matrix. Inputs should be in row-major form. In the code $\texttt{SIMD\_TILE}$ is $s$ and $\texttt{SW}$ is $\sigma$. $\texttt{TILE\_K}$ corresponds to the tiling mentioned in Exercise 1 and bounds checks are not implemented, so the kernel will only behave correctly when $n$ and $m$ are divisible by $8s\sigma$ and $k$ is divisible by $8\cdot\texttt{TILE\_K}$, see Exercise 2. To run this you'll need the async copy helper functions from the previous section in scope. The ~2.5 trillion 32-bit floating point operations a second mentioned in the first paragraph of this post was achieved with $\sigma=2$, $s=4$, and $\texttt{TILE\_K}=2$.

#include <metal_simdgroup_matrix>
#include <metal_compute>
using namespace metal;

template<ushort DIM>
inline void simdgroup_multiply(
  threadgroup float* A,
  threadgroup float* B,
  ushort2 c_pos,
  thread simdgroup_float8x8 &acc
) {
  simdgroup_float8x8 A_simd;
  simdgroup_float8x8 B_simd;
  #pragma clang loop unroll(full)
  for (ushort i = 0; i < DIM*8; i+=8) {
    simdgroup_load(A_simd, A, DIM*8, ulong2(i, c_pos.y));
    simdgroup_load(B_simd, B, SW*SIMD_TILE*8, ulong2(c_pos.x, i));
    simdgroup_multiply_accumulate(acc, A_simd, B_simd, acc);
  }
}

kernel void matmul(
  constant ushort& n,
  constant ushort& k,
  constant ushort& m,
  constant float& alpha,
  constant float& beta,
  const device float* A,
  const device float* B,
  device float* C,
  ushort3 t_pos    [[thread_position_in_grid]],
  ushort3 t_tg_pos [[thread_position_in_threadgroup]],
  ushort  s_pos    [[simdgroup_index_in_threadgroup]]
) {
  threadgroup float A_tg[SW*SIMD_TILE*8*TILE_K*8];
  threadgroup float B_tg[SW*SIMD_TILE*8*TILE_K*8];

  ushort2 c_origin = t_pos.yz*8*SIMD_TILE;
  ushort2 a_origin = ushort2(0,c_origin.y);
  ushort2 b_origin = ushort2(c_origin.x,0);

  simdgroup_float8x8 acc[SIMD_TILE][SIMD_TILE];
  for (ushort i=0; i<SIMD_TILE; i++)
      for (ushort j=0; j<SIMD_TILE; j++)
	acc[i][j] = simdgroup_float8x8(0);

  ushort k_tiles = k/(8*TILE_K);
  for (ushort l = 0; l < k_tiles; l++) {
    ushort2 a_pos = a_origin+ushort2(l*8*TILE_K,0);
    ushort2 b_pos = b_origin+ushort2(0,l*8*TILE_K);
    if (s_pos==0) {
      thread _simdgroup_event_t* events[2];
      events[0] = simdgroup_async_copy<TILE_K*8,SW*SIMD_TILE*8>(
        A,
        a_pos,
        ushort2(k,n),
        A_tg);
      events[1] = simdgroup_async_copy<SW*SIMD_TILE*8,TILE_K*8>(
        B,
        b_pos,
        ushort2(m,k),
        B_tg);
      __metal_wait_simdgroup_events(2,events);
    }
    threadgroup_barrier(mem_flags::mem_threadgroup);
    for (ushort i=0; i<SIMD_TILE; i++)
      for (ushort j=0; j<SIMD_TILE; j++)
	simdgroup_multiply<TILE_K>(
          A_tg,B_tg,
	  t_tg_pos.yz*8*SIMD_TILE+ushort2(i*8,j*8),
	  acc[i][j]);
    threadgroup_barrier(mem_flags::mem_none);
  }

  if (c_origin.x<m&&c_origin.y<n) {
    simdgroup_float8x8 c_simd;
    for (ushort i=0; i<SIMD_TILE; i++)
      for (ushort j=0; j<SIMD_TILE; j++) {
	ulong2 pos = ulong2(c_origin+ushort2(i*8,j*8));
	simdgroup_load(c_simd,C,m,pos);
	simdgroup_multiply(c_simd,c_simd, simdgroup_float8x8(beta));
	simdgroup_multiply_accumulate(c_simd,acc[i][j],simdgroup_float8x8(alpha),c_simd);
	simdgroup_store(c_simd,C,m,pos);
      }
  }
}

Code for running the kernel and the simdgroup_async_copy benchmark is avaliable here.

Thanks to Pete for freedom to explore during my PhD, the organizers for the GPU-mode discord server for talks that got my head around how a GPU works, Liu Liu for explaining metal-flash-attention, Ally for sanity and kindness, and Moses & Janita for patient listening and enchoragment to write this.